if(life){code();}

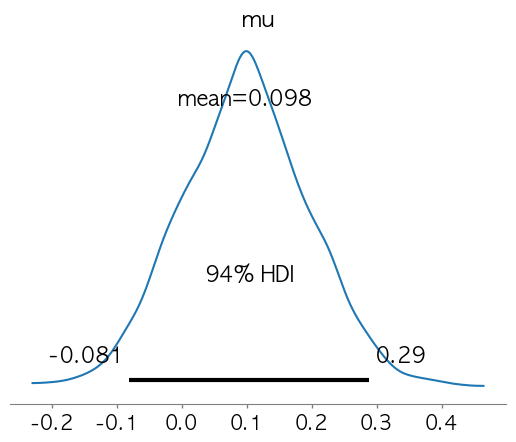
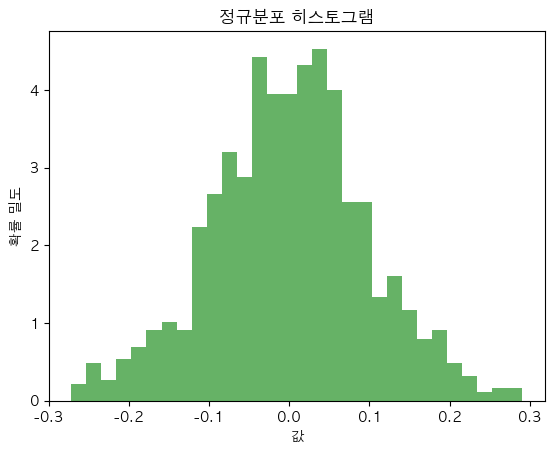
나이브 베이즈(Naive Bayes)  베이즈 정리(Bayes’ Theorem)를 기반으로 하는 확률 기반 머신러닝 분류 기법 (베이즈 정리 기반 확률적 분류 모델) "나이브(naive)"라는 이름이 붙은 이유→ 각 특징(feature)이 서로 독립적이라고 가정(Assumption)하기 때문 텍스트 분류(text classification), 스팸 필터링과 같은 분야에서 강력한 성능을 보임  베이즈 정리(Bayes'Theorem) 베이지안 통계베이즈 정리와 사전/사후 확률 베이즈 정리는 기존의 사전 확률을 새로운 증거를 바탕으로 갱신하여 사후 확률을 계산하는 방법을 제공→ 통계적 추론, 머신러닝, 의학적 진단 등 다양한 분야s2bibiprincess.tistory.com  나이브베이즈의 목적 주어진 데이..

베이즈 정리와 사전/사후 확률 베이즈 정리는 기존의 사전 확률을 새로운 증거를 바탕으로 갱신하여 사후 확률을 계산하는 방법을 제공→ 통계적 추론, 머신러닝, 의학적 진단 등 다양한 분야에서 활용 베이즈 정리P(A|B) = P(B|A) * P(A) / {P(B) 사전 확률 (Prior Probability, (P(A))): 새로운 정보를 얻기 전 특정 사건 (A) 가 발생할 확률우도 (Likelihood, (P(B|A))): 사건 (A) 가 발생했을 때 증거 (B) 가 나타날 확률사후 확률 (Posterior Probability, (P(A|B))): 증거 (B) 가 주어졌을 때 사건 (A) 가 발생할 확률증거 (Evidence, (P(B))): 증거 (B) 가 발생할 전체 확률 활용 사례조건부 확률 계산..

확률 특정 사건이 발생할 가능성0에서 1 사이의 값을 가짐  확률 값의 의미0: 불가능한 사건1: 반드시 발생하는 사건 확률의 기본 법칙 덧셈 법칙P(A or B) = P(A) + P(B) - P(A and B) 곱셈 법칙P(A and B) = P(A) * P(B|A)  확률의 활용사건 발생 가능성 계산리스크 분석 및 의사결정 트리 구성  확률 분포 데이터가 특정 확률에 따라 분포하는 형태를 의미 이항분포(Binomial Distribution) 성공/실패와 같은 두 가지 결과를 가지는 실험을 n번 독립적으로 수행하는 확률 분포 각 시행에서 성공 확률 p가 일정함성공 횟수를 X라 할 때, X는 이항분포를 따름: X ~B(n, p)평균: np, 분산: np(1-p)예동전 던지기제품의 불량 개수 예측 정규분..