베이즈 정리와 사전/사후 확률
베이즈 정리는 기존의 사전 확률을 새로운 증거를 바탕으로 갱신하여 사후 확률을 계산하는 방법을 제공
→ 통계적 추론, 머신러닝, 의학적 진단 등 다양한 분야에서 활용
베이즈 정리
P(A|B) = P(B|A) * P(A) / {P(B)
- 사전 확률 (Prior Probability, (P(A))): 새로운 정보를 얻기 전 특정 사건 (A) 가 발생할 확률
- 우도 (Likelihood, (P(B|A))): 사건 (A) 가 발생했을 때 증거 (B) 가 나타날 확률
- 사후 확률 (Posterior Probability, (P(A|B))): 증거 (B) 가 주어졌을 때 사건 (A) 가 발생할 확률
- 증거 (Evidence, (P(B))): 증거 (B) 가 발생할 전체 확률
활용 사례
- 조건부 확률 계산: 데이터 기반 의사 결정
- 스팸 필터링: 나이브 베이즈 분류기를 사용하여 이메일이 스팸인지 아닌지 판단
- 의료 진단: 질병의 사전 확률과 검사 결과를 활용하여 정확한 진단 가능
베이지안 추론
사전 확률을 새로운 데이터에 따라 갱신하는 방법론
모든 불확실성을 확률로 표현
→ 새로운 데이터를 지속적으로 반영하여 예측 성능을 향상하는 데 유용
베이지안 추론 과정
- 사전 분포 설정 (Prior Distribution): 초기 확률 분포를 설정
- 우도 계산 (Likelihood Calculation): 관측 데이터가 주어진 조건에서 발생할 확률을 계산
- 사후 분포 도출 (Posterior Distribution Calculation): 새로운 데이터를 반영하여 확률을 갱신
장점
- 작은 표본에서도 효과적
- 불확실성 정량화 가능
- 복잡한 모델에 적용 가능
단점
- 계산이 복잡할 수 있음
- 사전 분포 설정의 주관성이 존재
베이지안 통계의 응용
- 베이지안 네트워크: 확률적 그래프 모델을 사용하여 변수 간 관계 모델링
- 나이브 베이즈 분류기: 텍스트 분류, 스팸 필터링 등에 활용
- 베이지안 최적화: 하이퍼파라미터 튜닝에 사용
- 베이지안 딥러닝: 신경망의 가중치 불확실성을 모델링하여 신뢰성 있는 예측 수행
- 순차적 학습 및 온라인 학습: 데이터가 지속적으로 입력될 때 모델을 업데이트하는 방식
- 베이지안 모델 선택: 데이터에 가장 적합한 모델을 확률적으로 선택
PyMC를 활용한 간단한 베이지안 추론 예제
import pymc as pm
import numpy as np
import matplotlib.pyplot as plt
import arviz as az # arviz 추가
# 모델 정의
with pm.Model() as model:
mu = pm.Normal('mu', mu=0, sigma=1) # 사전 분포 설정
obs = pm.Normal('obs', mu=mu, sigma=1, observed=np.random.randn(100))
trace = pm.sample(1000, return_inferencedata=True) # 샘플링 수행
# 사후 분포 시각화
az.plot_posterior(trace) # arviz 사용
plt.show()
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [mu]
Progress Draws Divergences Step size Grad evals Sampling Speed Elapsed Remaining
─────────────────────────────────────────────────────────────────────────────────────────────────────────────────
━━━━━━━━━━━━━━━━━━━━━━━━ 2000 0 1.39 1 1475.48 draws/s 0:00:01 0:00:00
━━━━━━━━━━━━━━━━━━━━━━━━ 2000 0 1.05 1 1319.02 draws/s 0:00:01 0:00:00
━━━━━━━━━━━━━━━━━━━━━━━━ 2000 0 1.30 1 1179.29 draws/s 0:00:01 0:00:00
━━━━━━━━━━━━━━━━━━━━━━━━ 2000 0 1.45 1 1078.49 draws/s 0:00:01 0:00:00
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 2 seconds.
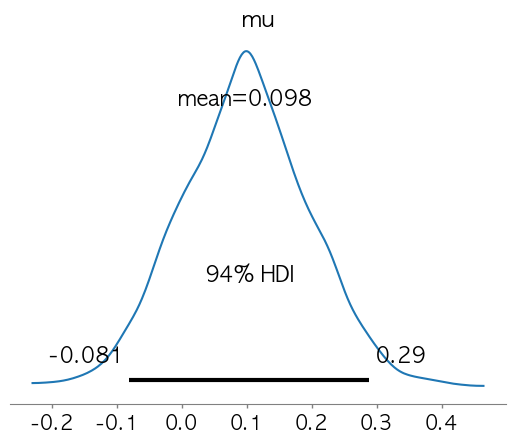
- 사전 분포 설정: μ ~ 𝓝(0,1) (정규 분포)
- 관측 데이터: 100개의 랜덤 샘플을 정규 분포에서 생성하여 입력
- 샘플링 수행: MCMC 방법을 사용하여 사후 분포 샘플링
- 사후 분포 시각화:
plot_posterior함수로 확인
베이지안 방법론의 확장
- 머신러닝: 베이지안 최적화를 통한 하이퍼파라미터 튜닝
- 딥러닝: 베이지안 신경망을 이용하여 모델의 불확실성 정량화
- 의료 통계: 신약 개발 및 임상 시험 분석
- 재무 분석: 확률적 자산 가격 모델링
베이지안 통계는 기존 빈도주의 통계보다 더 유연하고 강력한 방법론을 제공함
특히, 데이터가 적거나 불확실성이 높은 문제에서 효과적으로 활용가능
'인공지능을 위한 통계학 기초' 카테고리의 다른 글
| 통계적 추론과 가설 검증 (0) | 2025.02.22 |
|---|---|
| 확률과 확률 분포 (0) | 2025.02.21 |
| 데이터 상관관계 (0) | 2025.02.16 |
| 데이터 산포도 (1) | 2025.02.10 |
| 데이터 중심 지표- 평균(산술평균, 기하평균), 중앙값, 최빈값 (0) | 2025.02.02 |