t-SNE(t-Distributed Stochastic Neighbor Embedding)
고차원 데이터를 저차원(2D 또는 3D)으로 변환하여 시각화하는 차원 축소 기법
데이터 간 유사성을 보존하면서 고차원 데이터를 저차원으로 변환하여 데이터의 패턴을 효과적으로 시각화하는 데 활용
주로 비지도 학습에서 데이터의 구조를 이해하는 데 사용
- 비선형 구조 탐지 가능 → 데이터의 복잡한 구조도 효과적으로 표현
- 클러스터 시각화 → 데이터 내 잠지적 그룹(클러스터)을 명확히 구별할 수 있음
- 고차원 데이터 시각화 → 2차원 또는 3차원으로 변환하여 인간이 직관적으로 이해할 수 있도록 함
- 시간 복잡도가 높음 → 대규모 데이터셋에서는 계산이 느릴 수 있음
- 매번 다른 결과를 생성 → 초깃값(random_state)에 따라 결과가 달라질 수 있음
- 해석이 어려울 수 있음 → 거리 크기가 의미를 갖지 않으며 상대적 관계만 중요
작동원리
- 고차원 공간에서의 유사성 계산
데이터 포인트 간 거리를 기반으로 확률 분포 생성
비슷한 데이터 포인트일수록 높은 확률을 갖도록 설정 - 저차원 공간에서의 유사성 계산
고차원 데이터의 분포를 유지하기 위해 t-분포(t-distribution)를 활용하여 저차원 공간에서 유사성을 계산 - KL 발산(KL Divergence) 최소화
고차원과 저차원에서 계산한 유사성 확률 분포가 최대한 같아지도록 Kullback-Leibler발산(KL Divergence)을 최소화하는 방향으로 학습 - 반복적 최적화
데이터 포인트의 위치를 점진적으로 업데이트하며 최적의 저차원 표현을 찾음
t-SNE 실습
MNIST 데이터셋을 활용한 t-SNE 적용
데이터 로드
from sklearn.datasets import fetch_openml
import pandas as pd
# MNIST 데이터셋 불러오기
mnist = fetch_openml('mnist_784', version=1)
# 데이터와 레이블 분리
X = mnist.data # 이미지 데이터 (784개의 픽셀 값)
y = mnist.target # 숫자 라벨
# 데이터 프레임의 첫 5행 출력
print(X.head())
print(y.head())
"""
pixel1 pixel2 pixel3 pixel4 pixel5 pixel6 pixel7 pixel8 pixel9 \
0 0 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0 0 0
2 0 0 0 0 0 0 0 0 0
3 0 0 0 0 0 0 0 0 0
4 0 0 0 0 0 0 0 0 0
pixel10 ... pixel775 pixel776 pixel777 pixel778 pixel779 pixel780 \
0 0 ... 0 0 0 0 0 0
1 0 ... 0 0 0 0 0 0
2 0 ... 0 0 0 0 0 0
3 0 ... 0 0 0 0 0 0
4 0 ... 0 0 0 0 0 0
pixel781 pixel782 pixel783 pixel784
0 0 0 0 0
1 0 0 0 0
2 0 0 0 0
3 0 0 0 0
4 0 0 0 0
[5 rows x 784 columns]
0 5
1 0
2 4
3 1
4 9
Name: class, dtype: category
Categories (10, object): ['0', '1', '2', '3', ..., '6', '7', '8', '9']
"""
데이터 표준화
t-SNE는 거리 기반 학습 기법이므로, 데이터의 크기 차이를 줄이기 위해 표준화(Standardization) 과정이 필요
from sklearn.preprocessing import StandardScaler
# 데이터 표준화 (평균 0, 분산 1)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
t-SNE 수행
Scikit-learn의 TSNE를 사용하여 2차원 공간으로 차원 축소
from sklearn.manifold import TSNE
# t-SNE 모델 생성 (2차원으로 변환)
tsne = TSNE(n_components=2, random_state=42)
# t-SNE 학습 및 변환
X_tsne = tsne.fit_transform(X_scaled)
# 변환된 데이터의 크기 확인
print(X_tsne.shape)
"""
(70000, 2)
"""
t-SNE 결과 시각화
변환된 데이터를 2차원 그래프에서 시각화
데이터의 라벨(숫자 값)을 기반으로 색상을 구분
import matplotlib.pyplot as plt
import seaborn as sns
# 2차원 시각화
plt.figure(figsize=(10, 7))
sns.scatterplot(x=X_tsne[:, 0], y=X_tsne[:, 1], hue=y, palette='viridis', legend=None)
plt.title('t-SNE of MNIST Dataset (2D)')
plt.xlabel('t-SNE Component 1')
plt.ylabel('t-SNE Component 2')
plt.show()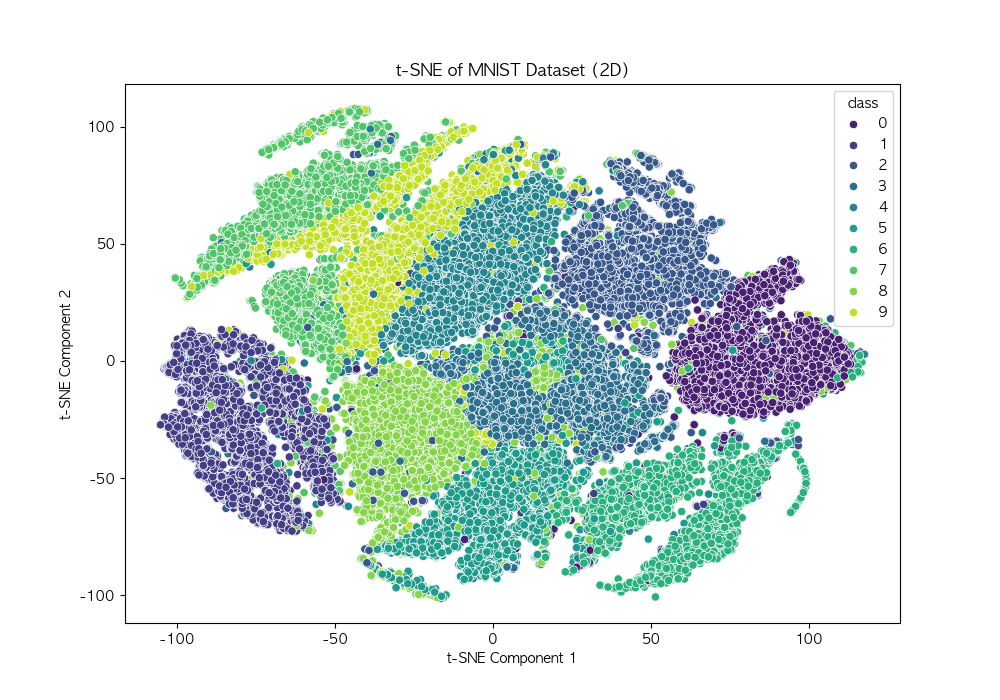
- 결과 그래프에서 비슷한 숫자들이 클러스터를 형성하는 것을 확인 가능
- t-SNE는 절대적인 거리 정보보다는 상대적 유사성만을 보존하기 때문에, 거리 크기 자체는 큰 의미가 없음
- 같은 숫자들은 가깝게 모여 있지만, 다른 숫자와의 경계가 완벽히 구분되지는 않을 수 있음
- 초기 조건(random_state)에 따라 결과가 달라질 수 있음 → 여러 번 실행하면서 최적의 결과를 찾는 것이 중요
t-SNE는 강력한 시각화 도구이지만, 해석이 중요함
클러스터가 형성되는 데이터라면 효과적으로 군집 구조 파악 가능
대규모 데이터에서는 시간이 오래 걸릴 수 있으므로, PCA로 미리 차원 축소 후 t-SNE를 적용하는 것도 고려 가능
결과는 매 실행마다 달라질 수 있으므로, 여러 번 수행하여 패턴을 확인하는 것이 중요
'⊢MachineLearning' 카테고리의 다른 글
| 앙상블 학습 : 배깅(Bagging)과 부스팅(Boosting) (0) | 2025.03.17 |
|---|---|
| 비지도학습 : 차원축소 - LDA(Linear Discriminant Analysis) (0) | 2025.03.17 |
| 비지도학습 : 차원축소 - PCA(Principal Component Analysis, 주성분 분석) (0) | 2025.03.17 |
| 비지도학습 : 군집화 모델 - DBSCAN (0) | 2025.03.17 |
| 비지도학습 : 군집화 모델 - 계층적 군집화 (2) | 2025.03.17 |