if(life){code();}

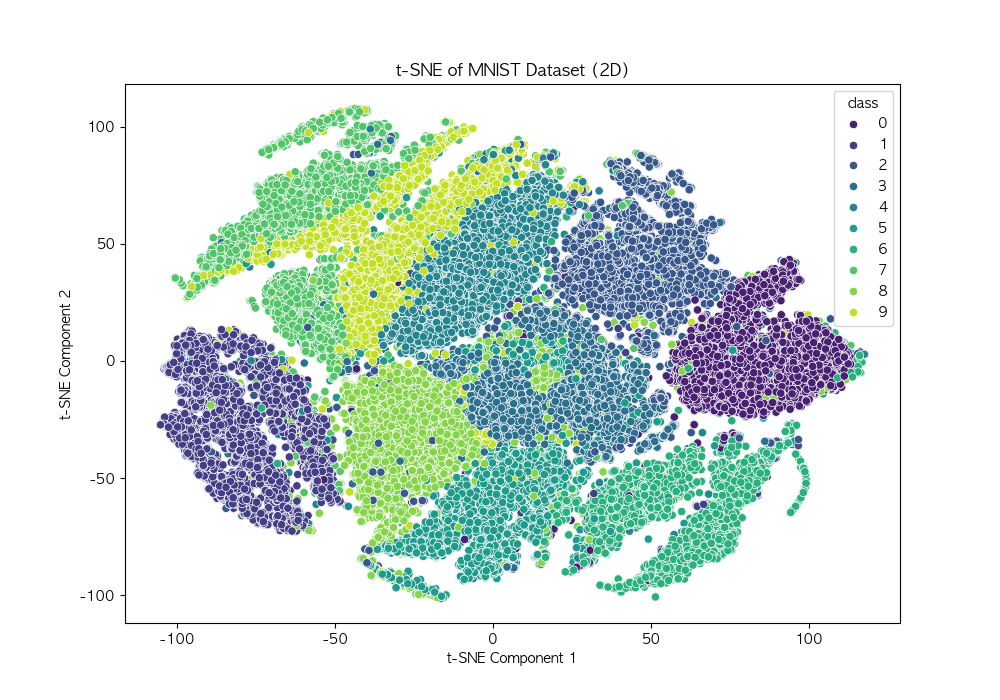
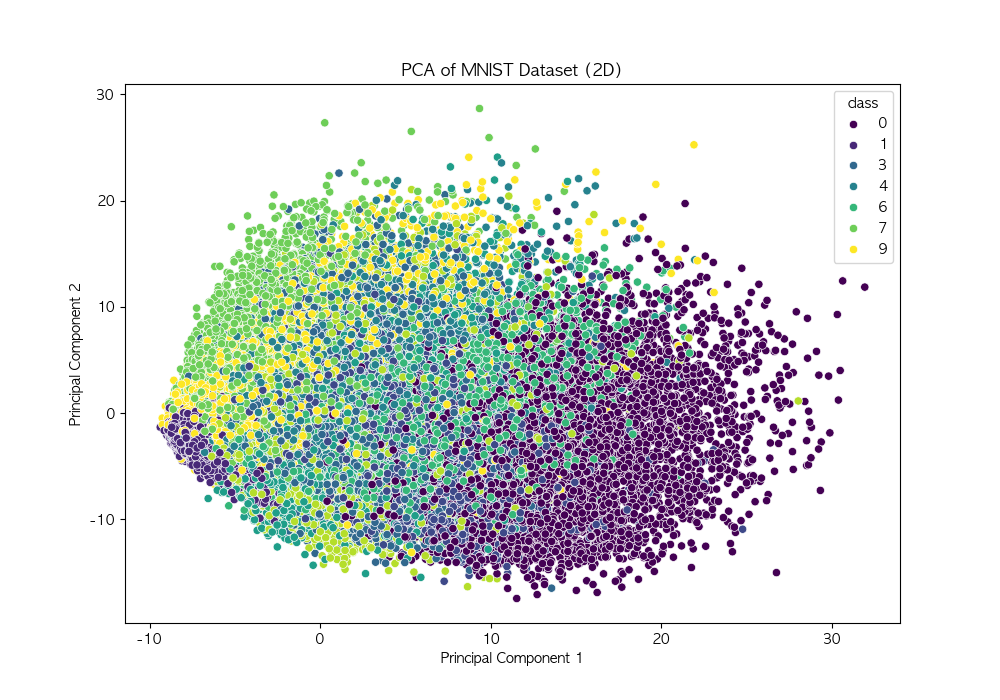
LDA (Linear Discriminant Analysis, 선형 판별 분석) 차원 축소와 분류를 동시에 수행하는 기법 클래스 간 분산을 최대화하고, 클래스 내 분산을 최소화하여 데이터를 변환저차원 공간에서 데이터의 구조를 유지하면서 분류 성능 향상 가능  작동 원리클래스별 평균 벡터 계산 : 각 클래스의 평균 벡터를 구함클래스 내 분산 행렬 계산 : 각 클래스 내부의 데이터 분산 계산클래스 간 분산 행렬 계산 : 클래스 평균 벡터 간의 분산을 구함고유값 및 고유벡터 계산 : 클래스 내 분산 행렬의 역행렬과 클래스 간 분산 행렬의 곱을 사용하여 고유값과 고유벡터 계산선형 판별 축 선택 : 고유값이 큰 순서대로 고유벡터를 정렬하여 주요한 선형 판별 축을 선택데이터 변환 : 선택된 판별 축을 사용하여 데이..

t-SNE(t-Distributed Stochastic Neighbor Embedding) 고차원 데이터를 저차원(2D 또는 3D)으로 변환하여 시각화하는 차원 축소 기법 데이터 간 유사성을 보존하면서 고차원 데이터를 저차원으로 변환하여 데이터의 패턴을 효과적으로 시각화하는 데 활용주로 비지도 학습에서 데이터의 구조를 이해하는 데 사용 비선형 구조 탐지 가능 → 데이터의 복잡한 구조도 효과적으로 표현클러스터 시각화 → 데이터 내 잠지적 그룹(클러스터)을 명확히 구별할 수 있음고차원 데이터  시각화 → 2차원 또는 3차원으로 변환하여 인간이 직관적으로 이해할 수 있도록 함 시간 복잡도가 높음 → 대규모 데이터셋에서는 계산이 느릴 수 있음매번 다른 결과를 생성 → 초깃값(random_state)에 따라 결과..

PCA(Principal Component Analysis, 주성분 분석) 고차원 데이터를 저차원으로 변환하는 차원 축소 기법 데이터의 분산을 최대한 보존하면서 주요 특징을 추출해 저차원 공간으로 변환이미지 압축 : 고차원 픽셀 데이터를 저차원으로 축소하여 공간 절약노이즈 제거 : PCA를 통해 데이터의 주요 특징만 남겨 노이즈 제거데이터 시각화 : 다차원 데이터를 2D 또는 3D로 변환하여 분석 작동 원리데이터 표준화(Standardization)각 특성의 평균을 0, 분산을 1로 맞춤공분산 행렬(Covariance Matrix) 계산데이터의 특성 간 관계 파악고유값(Eigenvalue) 및 고유벡터(Eigenvector) 계산공분산 행렬을 분해하여 주성분(Principal Component) 추출주성..