순환 신경망(Recrurrent Neural Network, RNN)

⊢ DeepLearning

순환 신경망(Recrurrent Neural Network, RNN)

최 수빈 2025. 3. 20. 00:21

순환 신경망(Recurrent Neural Network, RNN)

시계열 데이터 및 순차적 데이터를 처리하기 위한 신경망

이전 시간 단계의 정보를 현재 시간 단계로 전달하여 시퀀스 패턴을 학습

주식 가격 예측, 날씨 예측, 텍스트 생성 등에 적합

동작 원리

순환 구조 : 입력 데이터와 이전 은닉 상태(hidden state)를 받아 현재 은닉 상태를 출력
가중치 공유 : 모든 시간 단계에서 동일한 가중치를 사용하여 계산
역전파(BPTT, Backpropagation Through Time)을 통해 학습 진행

→ 과거의 정보가 너무 오래되면 영향을 거의 미치지 못하는 장기 의존성 문제(long-term dependency problem) 발생

기울기 소실(Vanishing Gradient) 문제
RNN의 역전파 과정에서 기울기가 시간이 지날수록 점점 작아져 0에 수렴하는 현상
→ 초반의 입력 정보는 네트워크가 학습하지 못하게 되어 긴 시퀀스를 처리하기 어려워짐
기울기 폭발(Exploding Gradient) 문제
기울기가 너무 커져서 가중치가 비정상적으로 커지는 문제
기울기 클리핑(Gradient Clipping) 기법을 사용하여 해결
단기 기억(Bias Towards Short-Term Memory)
입력이 많아질수록 초반 정보는 점점 희미해짐

LSTM & GRU

RNN이 겪는 장기 의존성 문제(long-term dependency problem)를 해결하기 위해 LSTM과 GRU가 개발됨

LSTM(Long Short-Term Memory)

셀 상태(cell state)와 게이트(gate) 구조를 도입, 장기 의존성을 효과적으로 학습가능

→ 셀 상태와 은닉 상태를 모두 사용 (더 복잡한 게이트 구조를 가짐)

입력 게이트(input gate), 출력 게이트(output gate), 망각 게이트(forget gate)를 사용하여 정보 조절

GRU(Gated Recurrent Unit)

LSTM의 변형

셀 상태 대신 은닉 상태(hidden state)만을 사용하여 구조를 단순화 함

업데이트 게이트(update gate)와 리셋 게이트(reset gate)를 사용하여 정보를 조절

LSTM vs. GRU

모델	사용 메모리	연산 속도	학습 성능
LSTM	높음	느림	장기 의존성 학습에 강함
GRU	낮음	빠름	비교적 간단한 문제에 적합

RNN을 이용한 시계열 데이터 처리 방법

데이터 전처리
시계열 데이터를 적절한 형태로 변환하고, 정규화(normalization)
입력 시퀀스와 출력 시퀀스 정의
모델 구축
RNN, LSTM, GRU 등의 모델을 정의
입력 크기, 은닉 상태 크기, 출력 크기 등을 설정
모델 학습
손실 함수와 최적화 알고리즘을 정의
순전파와 역전파를 통해 모델을 학습시킴
모델 평가
테스트 데이터를 사용하여 모델의 성능을 평가

RNN과 LSTM을 이용한 시계열 데이터 예측 (PyTorch)

PyTorch를 활용하여 Sine 파형을 예측하는 RNN과 LSTM 모델 구축

RNN/LSTM을 활용한 시계열 데이터 예측 과정

데이터셋 생성 및 전처리: Sine 함수 데이터 생성
모델 구축: RNN 및 LSTM 모델 정의
모델 학습: MSE 손실 함수 사용 및 Adam 최적화 적용
모델 평가 및 시각화: 예측 결과를 비교하여 시각적으로 확인

라이브러리 임포트

import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np 
import matplotlib.pyplot as plt

데이터셋 생성 및 전처리

# Sine 파형 데이터 생성
def create_sine_wave_data(seq_length, num_samples):
    X, y = [], []
    for _ in range(num_samples):
        start = np.random.rand()  # 시작점을 랜덤하게 설정 (0~1 사이 값)
        x = np.linspace(start, start + 2 * np.pi, seq_length) # 일정한 간격으로 seq_length만큼 데이터 생성
        X.append(np.sin(x)) # 현재 x값의 sine 값을 입력 데이터로 사용
        y.append(np.sin(x + 0.1))  # x에서 0.1만큼 이동한 값을 정답 데이터로 사용 (예측 목표)
    return np.array(X), np.array(y)

seq_length = 50 # 한 시퀀스의 길이 (50개 데이터)
num_samples = 1000 # 생성할 시퀀스의 개수 (1000개)
X, y = create_sine_wave_data(seq_length, num_samples)

# PyTorch 텐서 변환 (batch_size, seq_length, input_size)
X = torch.tensor(X, dtype=torch.float32).unsqueeze(-1) # .unsqueeze(-1) : 마지막 차원 추가
y = torch.tensor(y, dtype=torch.float32).unsqueeze(-1)

RNN 모델 정의

class SimpleRNN(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(SimpleRNN, self).__init__()
        self.rnn = nn.RNN(input_size, hidden_size, batch_first=True) # 기본 RNN 레이어 정의
        self.fc = nn.Linear(hidden_size, output_size) # 은닉 상태를 최종 출력값으로 변환

    def forward(self, x):
        h0 = torch.zeros(1, x.size(0), hidden_size) # 초기 은닉 상태 (num_layers=1)
        out, _ = self.rnn(x, h0) # RNN 연산 수행
        out = self.fc(out) # 전체 시퀀스에 대해 출력 생성
        return out

input_size = 1
hidden_size = 32
output_size = 1
model = SimpleRNN(input_size, hidden_size, output_size)

nn.RNN : 순환 신경망(RNN)층을 정의

nn.RNN(input_size, hidden_size, batch_first) : 입력크기, 은닉 상태 크기, 배치 차원을 첫 번째로 설정

nn.Linear : 선형 변환을 적용하는 완전 연결(fully connected) 레이어를 정의

nn.Linear(in_features, out_features) : 입력 특징의 수와 출력 특징의 수를 지정

모델 학습

# 손실 함수와 최적화 알고리즘 정의
criterion = nn.MSELoss()  # 평균 제곱 오차 손실 함수
optimizer = optim.Adam(model.parameters(), lr=0.01)  # Adam 최적화 사용

num_epochs = 100 # 100번 학습 진행
for epoch in range(num_epochs):
    outputs = model(X)  # 모델 예측값 생성
    optimizer.zero_grad()  # 기울기 초기화
    loss = criterion(outputs, y)  # 손실 계산
    loss.backward()  # 역전파 수행
    optimizer.step()  # 최적화 수행 (가중치 업데이트)

    if (epoch + 1) % 10 == 0:
        print(f'Epoch [{epoch + 1}/{num_epochs}], Loss: {loss.item():.4f}')  # 10 epoch마다 손실 출력
        
print('Finished Traning')

"""
Epoch [10/100, Loss: 0.0236
Epoch [20/100, Loss: 0.0043
Epoch [30/100, Loss: 0.0022
Epoch [40/100, Loss: 0.0015
Epoch [50/100, Loss: 0.0013
Epoch [60/100, Loss: 0.0011
Epoch [70/100, Loss: 0.0009
Epoch [80/100, Loss: 0.0008
Epoch [90/100, Loss: 0.0007
Epoch [100/100, Loss: 0.0006
Finished Training
"""

모델 평가 및 시각화

model.eval() # 평가 모드 전환
with torch.no_grad():
    predicted = model(X).detach().numpy()  # 텐서를 계산 그래프에서 분리, 예측값을 NumPy 배열로 변환

plt.figure(figsize=(10, 7))
plt.plot(y.numpy().flatten()[:100], label='True')  # 실제 값
plt.plot(predicted.flatten()[:100], label="Predict")  # 예측 값
plt.legend()
plt.show()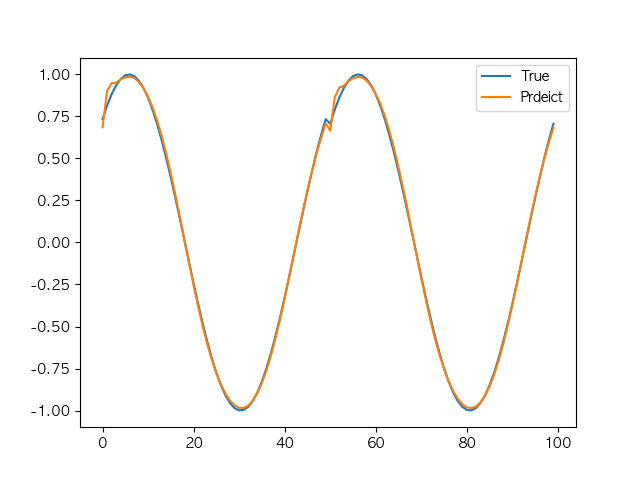

LSTM 모델 정의

class SimpleLSTM(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(SimpleLSTM, self).__init__()
        self.lstm = nn.LSTM(input_size, hidden_size, batch_first=True) # LSTM 레이어 정의
        self.fc = nn.Linear(hidden_size, output_size) # 은닉 상태를 최종 출력값으로 변환

    def forward(self, x):
        h0 = torch.zeros(1, x.size(0), hidden_size) # 초기 은닉 상태
        c0 = torch.zeros(1, x.size(0), hidden_size) # 초기 셀 상태
        out, _ = self.lstm(x, (h0, c0)) # LSTM 연산 수행
        out = self.fc(out) 
        return out

model = SimpleLSTM(input_size, hidden_size, output_size)

nn.LSTM : 장단기 메모리(LSTM) 층을 정의

nn.LSTM(input_size, hidden_size, batch_first) : 입력 크기, 은닉 상태 크기, 배치 차원을 첫 번째로 설정

모델 학습

# 손실 함수와 최적화 알고리즘 정의
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=0.01)

num_epochs = 100
for epoch in range(num_epochs):
    outputs = model(X)
    optimizer.zero_grad()
    loss = criterion(outputs, y)
    loss.backward()
    optimizer.step()

    if (epoch + 1) % 10 == 0:
        print(f'Epoch [{epoch + 1}/{num_epochs}], Loss: {loss.item():.4f}')

print('Finished Training')

"""
Epoch [10/100, Loss: 0.0560
Epoch [20/100, Loss: 0.0155
Epoch [30/100, Loss: 0.0044
Epoch [40/100, Loss: 0.0036
Epoch [50/100, Loss: 0.0023
Epoch [60/100, Loss: 0.0020
Epoch [70/100, Loss: 0.0016
Epoch [80/100, Loss: 0.0013
Epoch [90/100, Loss: 0.0011
Epoch [100/100, Loss: 0.0010
Finished Training
"""

모델 평가 및 시각화

model.eval()
with torch.no_grad():
    predicted = model(X).detach().numpy()

plt.figure(figsize=(10, 5))
plt.plot(y.numpy().flatten()[:100], label='True')
plt.plot(predicted.flatten()[:100], label='Predicted')
plt.legend()
plt.show()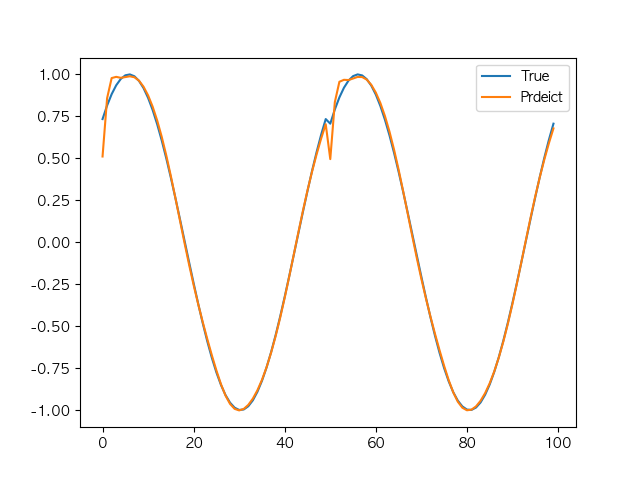

→ 현재 코드에서 RNN이 LSTM보다 성능이 좋음

시퀀스 길이가 짧아서 장기 의존성이 필요 없음
Sine 파형 데이터가 단순한 주기적 패턴이기 때문에 복잡한 기억 장치(LSTM)가 필요 없음
RNN이 더 가볍고 빠른 모델이라 학습이 빠르게 진행됨
LSTM은 더 복잡한 구조이기 때문에, 적은 데이터에서의 과적합 가능성

상기 이유로, Sine데이터 같은 단순한 패턴에서는 RNN이 오히려 더 좋은 성능을 보임

저작자표시 비영리 변경금지

'⊢ DeepLearning' 카테고리의 다른 글

자연어 처리(Natural Language Processing, NLP) 모델 (0)	2025.03.20
어텐션(Attention) 메커니즘 (1)	2025.03.20
합성곱 신경망(Convolutional Neural Network, CNN) (5)	2025.03.20
인공 신경망(Artificial Neural Network, ANN) (0)	2025.03.19
딥러닝 실습 환경 구축 (0)	2025.03.18

현재글순환 신경망(Recrurrent Neural Network, RNN)

if(life){code();}

life: Compiling… Please Wait

250x250

if(life){code();}